Maschinenbau-Student.de

.

Symmetrie

.

Gesucht ist, ob die folgenden Funktionen Symmetrisch sind.

 

1.

f(x)=

x+1

x-1

 

2.

f(x)=

2x²+3x-4

x²

 

3.

f(x)=

x³-2x²-3x

x-2

 

4.

f(x)=

x³-2x²+x

 

5.

f(x)=

x²+4x+4

x+2

 

6.

f(x)=

x²+3

x

7. f(x)=-2(x²)²+5x²+2

Eine Funktion ist dann Symmetrisch, wenn

f(-x)=f(x) ist. Dann spricht man von Spiegelsymmetrie. Ein Beispiel dafür wäre

f(x)=x² , weil egal welches Vorzeichen ein

x-Wert hat (Negativ oder Positiv), kommt immer der selbe y-Wert raus. Dass heißt die Funktion ist spiegelsymmetrisch zur y-Achse. (siehe Bild)
.  

Eine Funktion ist auch noch Symmetrisch, wenn

f(-x)=-f(x) ist. Dann spricht man von Punktsymmetrie. Ein Beispiel dafür wäre f(x)=x³ , weil bei negativen oder positiven x-Wert, der selbe y-Wert, nur mit unterschiedlichen Vorzeichen, herauskommt. Dass heißt die Funktion ist punktsymmetrisch zum Koordinatenursprung. (siehe Bild)

 

1.Die Funktion ist weder spiegelsymmetrisch zur y-Achse, noch punktsymmetrisch zum Koordinatenursprung, weil bei der Berechnung des y-Wertes mit zum Beispiel x=2 und x=-2, unterschiedliche y-Werte herauskommen.

 

2.  Die Funktion ist weder spiegelsymmetrisch zur y-Achse, noch punktsymmetrisch zum Koordinatenursprung, weil bei der Berechnung des y-Wertes mit zum Beispiel x=1 und x=-1, unterschiedliche y-Werte herauskommen.

 

3.  Die Funktion ist weder spiegelsymmetrisch zur y-Achse, noch punktsymmetrisch zum Koordinatenursprung, weil bei der Berechnung des y-Wertes mit zum Beispiel x=1 und x=-1, unterschiedliche y-Werte herauskommen.

 

4.  Die Funktion ist weder spiegelsymmetrisch zur y-Achse, noch punktsymmetrisch zum Koordinatenursprung, weil bei der Berechnung des y-Wertes mit zum Beispiel x=1 und x=-1, unterschiedliche y-Werte herauskommen.

  

5.  Die Funktion ist weder spiegelsymmetrisch zur y-Achse, noch punktsymmetrisch zum Koordinatenursprung, weil bei der Berechnung des y-Wertes mit zum Beispiel x=1 und x=-1, unterschiedliche y-Werte herauskommen.

 

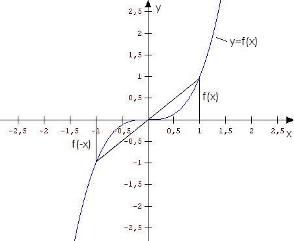
6.  Die Funktion ist punktsymmetrisch zum Koordinatenursprung, weil bei der Berechnung des y-Wertes mit zum Beispiel x=1 und x=-1, für x=1 der y-Wert 4 herauskommt und für x=-1 der y-Wert -4 herauskommt.

 

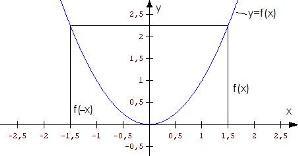
7.  Die Funktion ist spiegelsymmetrisch zur y-Achse, weil bei der Berechnung des y-Wertes mit zum Beispiel x=1 und x=-1, für x=1 der y-Wert 5 herauskommt und für x=-1 der y-Wert 5 herauskommt.

Alle Angaben ohne Gewähr auf Richtigkeit. Falls sie einen Fehler gefunden haben schreiben sie uns bitte eine E-Mail unter Kontakt.